![]()
기수 정렬 기수 정렬은 배열 안의 데이터가 모두 n자릿수 이하의 자연수인 경우 사용 가능한 정렬이다. 일의 자릿수로 크기 비교후 정렬하고 다음은 십의 자리, 백의 자리,...해서 n자릿수까지 크기를 비교하는 독특한 정렬이다. 시간 복잡도는 O(dn)으로 빠른 편이다. 다만 테이블이 따로 필요하다는 단점이 있다. 기수 정렬이 어떤 순서로 동작하는지는 아래의 영상에 나와있다. https://youtu.be/nu4gDuFabIM import java.io.*; import java.util.*; class Radix { static void countSort(int arr[], int n, int exp) { int output[] = new int[n]; int i; int count[] = new int[..
![]()
힙 정렬은 자료구조의 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법이다. 각각의 차이는 내림차순이냐 오름차순이냐에 있다. 트리 구조를 이용해서 작성할 필요는 없고 간단하게 1차원 배열로도 충분히 표현 가능하다. 정렬해야 할 값을 배열에 저장하고 힙 삽입을 통해 차례대로 삽입한다. 이 과정이 끝나면 힙이 구성되는데 배열에서 최소값부터 삭제하면서 정렬한다. 위의 그림은 최대 힙 정렬을 하는 과정을 보여준다. 부모노드와 자식노드의 크기 비교를 해서 오름차순, 내림차순에 맞게 삽입을 하면서 힙을 구성한다. 다음에는 부모노드를 제거하고 그 자리에 최하위 자식 노드를 삽입한다. 다시 루트 노드의 자식 노드와 크기 비교를 하며 힙을 재구성한다. 이 과정을 반복하면 힙 정렬이 끝난다. 힙 정렬의 시간 복잡도..
![]()
퀵정렬은 병합 정렬처럼 분할 정복 알고리즘에 속하지만 병합 정렬과는 달리 불안정 정렬이다. 배열에 있는 값중 아무거나 하나를 pivot으로 정한다. 이를 값을 기준으로 pivot보다 작은 값은 왼쪽으로 큰 값은 오른쪽으로 정렬한다.(오름차순 정렬) 이렇게 pivot을 기준으로 왼쪽과 오른쪽으로 분할된 배열로 위의 과정을 반복한다. 퀵 정렬의 시간 복잡도는 O(nlogn)으로 병합 정렬과 동일하다. import java.util.Random; public class Quick { public static void quickSort(int[] a,int p,int r) { int q; if(p
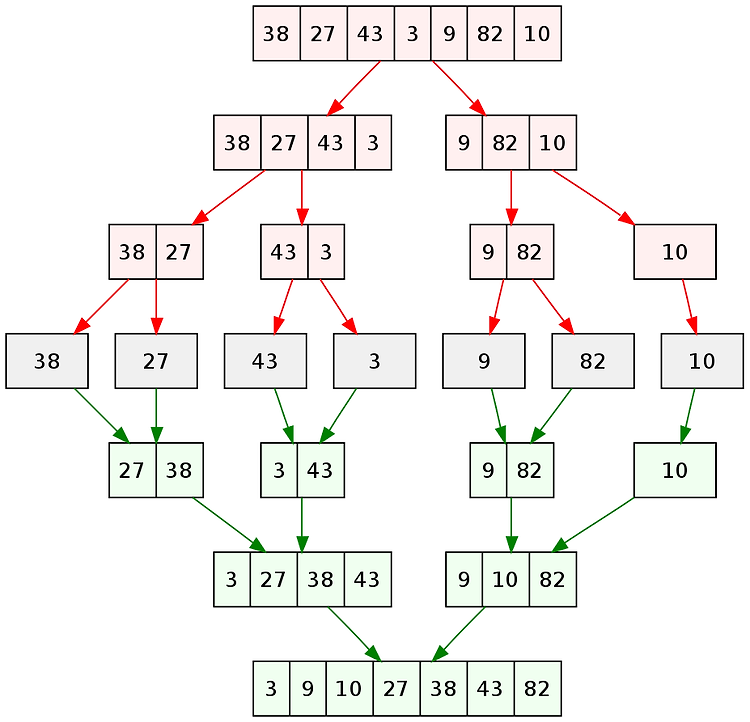
![]()
Merge Sort 번역하기에 따라 병합 정렬 혹은 합병 정렬이라고 불린다. 분할 정복 알고리즘의 하나로 배열을 잘게 쪼개서 정렬을 하고 이를 합치는 방식이다. 말로 설명하기보다 그림으로 이해하는 것이 더 편하다. 아래와 같은 7size의 배열이 있다고 가정하자. 이를 4size의 배열과 3size의 배열로 나눈다. 다시 4size배열을 2size의 배열 두개로 나누고,... size가 하나가 될때까지 반복한다. 이후 각각을 비교해서 합치면서 정렬된 7size의 배열로 만들어준다. Merge Sort의 시간 복잡도는 O(nlogn)가 된다. public class merge { public static void mergeSort(int[] a,int p,int r) { int q = (int)Math.f..
![]()
삽입 정렬을 설명할때 보통 카드 게임에서 카드를 정렬하는 방식과 같다고 말한다. 0번 인덱스와 1번 인덱스를 비교하여 정렬한다. 이후 0,1,2를 비교해서 자리를 찾는다. 그 다음은 3번 인덱스가 들어갈 자리를 찾고 이런 식으로 끝까지 비교한다. 정렬된 배열에서 지정한 자리에 자료를 삽입하여 정렬하므로 삽입 정렬이라고 부른다. 단 초기 Key값을 0번 인덱스의 값이 아닌 1번 인덱스의 값으로 지정한다. 삽입 정렬의 시간 복잡도 또한 O(n2)로 버블,선택 정렬과 동일하다. 이 과정을 자바 코드로 표현하면 아래와 같다. public class insert { public static void insertSort(int[] a){ int N = a.length; int key; int i,j; for (i ..
![]()
선택 정렬은 0번 인덱스를 마지막번 인덱스까지 차례대로 비교해 가장 작은 값을 찾아 0번에 놓고, 1번 인덱스를 차례대로 비교해 그 중 가장 작은 값을 찾아 1번에 놓는 과정을 반복하며 정렬을 수행한다. 1회전을 수행하고 나면 최소값이 맨 앞에 오게 되므로 2회전에서는 맨 앞인 0번 인덱스를 빼고 정렬을 진행하면 된다. 선택 정렬의 성능 분석 공식은 T(n) = (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)로 버블정렬과 동일하다. 5 3 1 4 2를 가지고 선택 정렬을 수행하는 과정은 위의 이미지와 같다. 최소값을 담아둘 임의의 변수 min값이 필요함을 알 수 있다. 자바로 작성하면 다음과 같다. public class Selection { public static v..
![]()
버블 정렬은 배열의 0번 인덱스와 1번 인덱스를 비교하고 1번 인덱스와 2번 인덱스를 비교하는 과정을 처음부터 마지막 인덱스까지 반복하여 진행한다. 즉 인접 인덱스를 비교하면서 정렬하는 방식이다. 1회전을 수행하고 나면 제일 큰 숫자가 맨 뒤에 위치하게 된다. 따라서 다음 회전에서는 마지막 인덱스-1까지만 고려한다. 버블 정렬의 성능 분석 공식은 S(n) + S(n-1) + … + S(2) = (n-1) + (n-2) + (n-3) + … + 3 + 2 + 1 가 된다. 여기서의 S(n)은 인덱스 비교하는 시간 = 교환하는 시간이라고 한다. 식을 정리하면 O(n^2) 임을 알 수 있다. 위의 이미지에서는 5 3 1 4 2 의 자료를 정렬하는 과정을 보여주고 있다. 이를 자바 소스 코드로 작성하면 다음과 ..