신장 트리란
그래프 중 모든 정점이 간선으로 연결되어 있되, 간선간의 사이클이 없는 그래프
최소 비용 신장 트리
각 간선에 비용(가중치 합)이 있을때 최소화 하는 신장트리를 말함
크루스칼 알고리즘
1. 간선들을 가중치의 오름차순으로 정렬
2. 사이클을 형성하지 않는 간선 선택
3. 해당 간선을 현재의 집합에 추가
즉 간선을 중심으로 탐색을 합니다.
아래는 이해하기 쉽게 gif 이미지를 가져왔다. be간선을 연결하려고 하면 이는 사이클을 형성하기에 제외하는 것을 볼 수 있다.
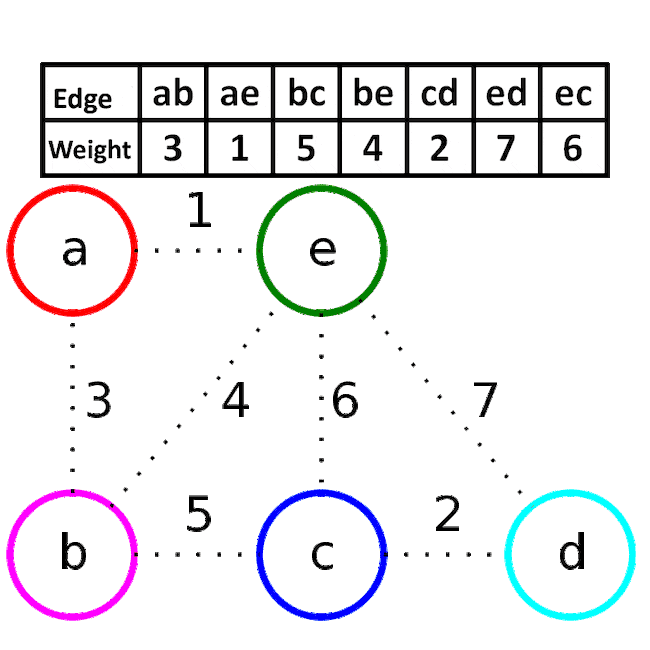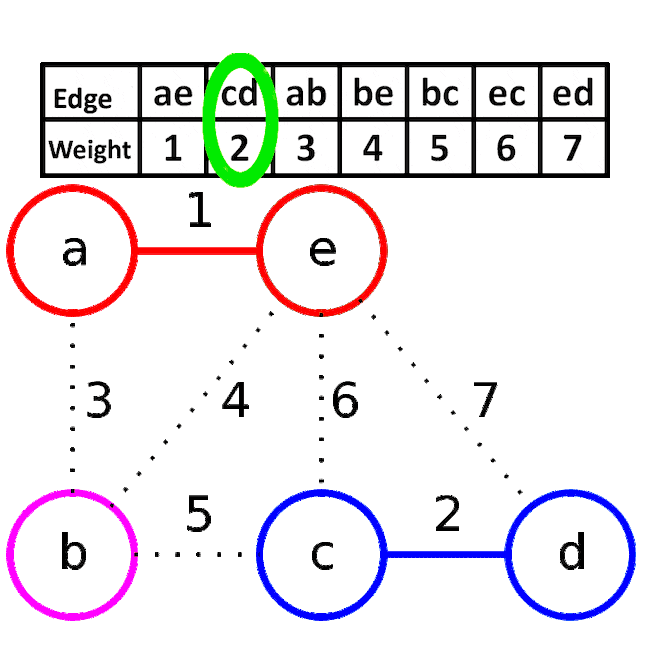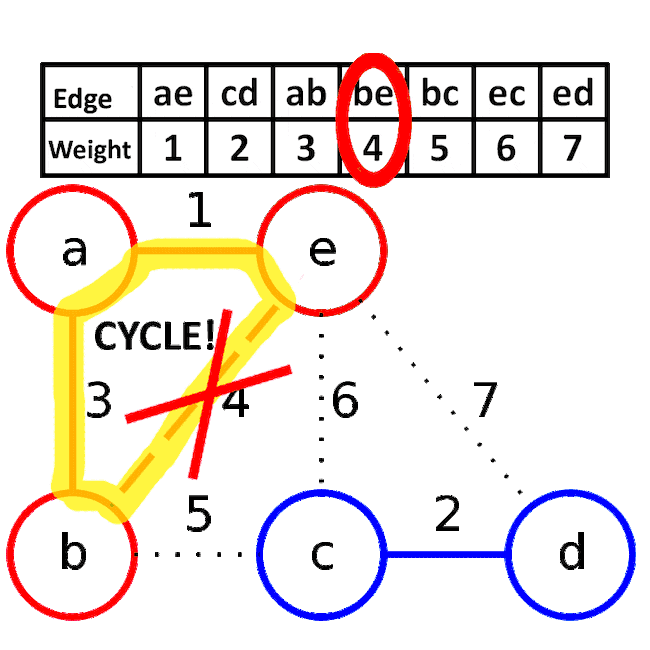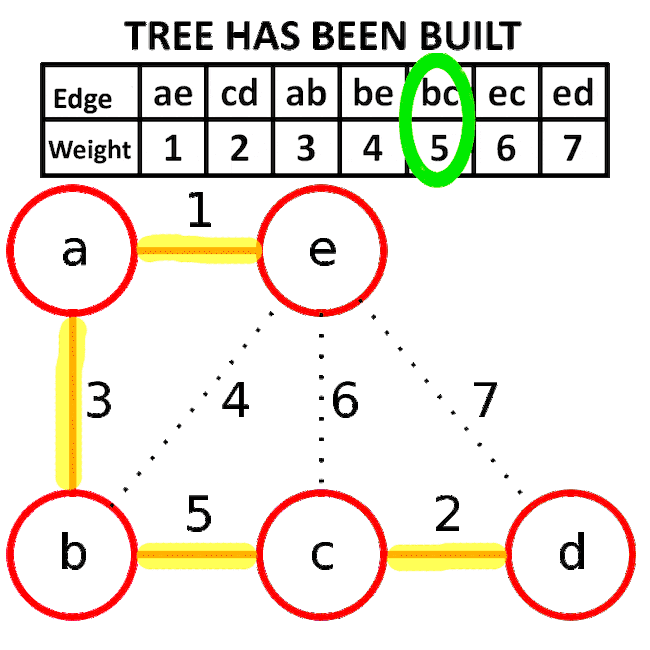
MST의 대표 알고리즘인 프림 알고리즘과 크루스칼 알고리즘을 비교하면 아래와 같다.
| 크루스 알고리즘 | 프림 알고리즘 |
| 간선을 기반으로 하는 알고리즘 | 정점을 기반으로 하는 알고리즘 |
| 전단계에서 만들어진 신장트리와는 상관없이 무조건 최저 간선만을 선택하는 방법 | 전단계에서 만들어진 신장트리를 확장하는 방법 |
| 희박한 그래프를 대상으로할 때 유리(에지수가 적은 그래프) | 밀집한 그래프를 대상으로할 때 유리(에지수가 많은 그래프) |
구현
import java.util.Arrays;
public class KruskalMSTGraph {
class Edge implements Comparable<Edge> {
int src, dest, weight;
@Override
public int compareTo(Edge compareEdge) {
return this.weight - compareEdge.weight;
}
}
class subset {
int parent, rank;
}
int V, E;
Edge edge[];
KruskalMSTGraph(int v, int e) {
V = v;
E = e;
edge = new Edge[E];
for (int i = 0; i < e; ++i) {
edge[i] = new Edge();
}
}
int find(subset subsets[], int i) {
if (subsets[i].parent != i) {
subsets[i].parent = find(subsets, subsets[i].parent);
}
return subsets[i].parent;
}
void Union(subset subsets[], int x, int y) {
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if (subsets[xroot].rank < subsets[yroot].rank) {
subsets[xroot].parent = yroot;
} else if (subsets[xroot].rank > subsets[yroot].rank) {
subsets[yroot].parent = xroot;
} else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
void KruskalMST() {
Edge result[] = new Edge[V];
int e = 0;
int i = 0;
for (i = 0; i < V; ++i) {
result[i] = new Edge();
}
Arrays.sort(edge);
subset subsets[] = new subset[V];
for (i = 0; i < V; ++i) {
subsets[i] = new subset();
}
for (int v = 0; v < V; ++v) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
i = 0;
while (e < V - 1) {
Edge next_edge = new Edge();
next_edge = edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
if (x != y) {
result[e++] = next_edge;
Union(subsets, x, y);
}
}
for (i = 0; i < e; ++i) {
System.out.println(result[i].src + " -- " + result[i].dest + " == " + result[i].weight);
}
}
public static void main(String[] args) {
int V = 4;
int E = 5;
KruskalMSTGraph graph = new KruskalMSTGraph(V, E); // add edge 0-1
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = 10; // add edge 0-2
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 6; // add edge 0-3
graph.edge[2].src = 0;
graph.edge[2].dest = 3;
graph.edge[2].weight = 5; // add edge 1-3
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 15; // add edge 2-3
graph.edge[4].src = 2;
graph.edge[4].dest = 3;
graph.edge[4].weight = 4;
graph.KruskalMST();
}
}[참고]
크러스컬 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 컴퓨터 과학에서, 크러스컬 알고리즘(영어: Kruskal’s algorithm)은 최소 비용 생성나무를 찾는 알고리즘이다. 변의 개수를 E {\displaystyle E} , 꼭짓점의 개수를 V {\displaystyle V} 라고 하면 이 알고리즘은 O ( E log V ) {\displaystyle {\color {Blue}O}(E\log V)} 의 시간복잡도를 가진다. 크러스컬 알고리즘은 아래의 순서대로 작동한다
ko.wikipedia.org
https://blog.naver.com/PostView.nhn?blogId=ssarang8649&logNo=221038259400
최소 신장 트리 크루스칼 알고리즘 JAVA로 구현해보기 - Minimum Spanning Tree(MST) Kruskal
안녕하세요. 이번 포스팅은 이전의 MST 프림 알고리즘에 이어서 더 많이 쓰이는 최소 신장 트리 알고리...
blog.naver.com
'알고리즘 > 이론' 카테고리의 다른 글
| 세그먼트 트리(Segment Tree) (0) | 2021.05.11 |
|---|---|
| [JAVA] 이진트리 탐색 dfs(중위 탐색)와 bfs 구현하기 (0) | 2021.04.20 |
| 그래프 표현 방식과 탐색 방법 (0) | 2019.05.19 |
| Dynamic Programming (0) | 2019.05.04 |
| Hash 함수 (2) | 2019.04.30 |
