이진 트리
계층 구조인 트리의 자식이 left, right 둘로 이루어진 형태를 이진 트리라고 합니다.

이진 트리를 구성하고 dfs와 bfs로 탐색하는 예제를 작성하는 것이 이 포스팅의 목표입니다.
그림에서 초록 원들을 각각 노드라고 부릅니다. 각 노드들이 가지를 뻗듯이 연결되어 있으니(같은 이유로 트리라는 이름이 붙여졌습니다.) Node의 값과 연결된 노드들의 정보가 필요하겠죠. 즉 Node 클래스에는 다음과 같은 필드가 필요합니다.
public class Node{
int value;
Node left;
Node right;
...
}
생성자는 직접 만들어보세요.
DFS
DFS는 깊이 우선 탐색이라고 부릅니다. 트리에서의 깊이는 맨 위에 있는 노드(루트 노드)로 부터 특정 노드까지의 길이를 깊이라고 말합니다. 깊이 우선 탐색은 한쪽으로 깊게 쭈우우욱 파고 들어가고 그 근처 노드를 탐색하는 방식입니다. 이 깊이 우선 탐색에는 3가지 방식이 더 있답니다.
전위 순회
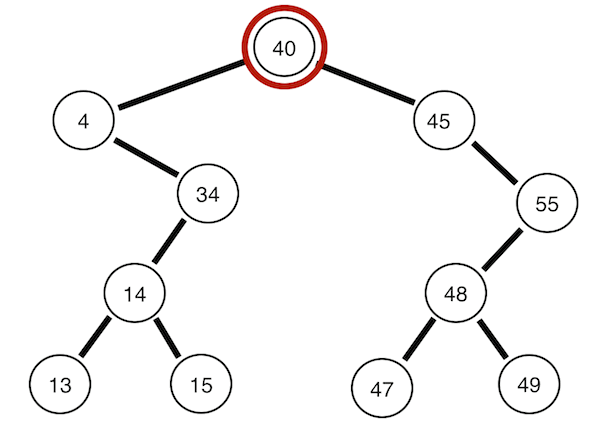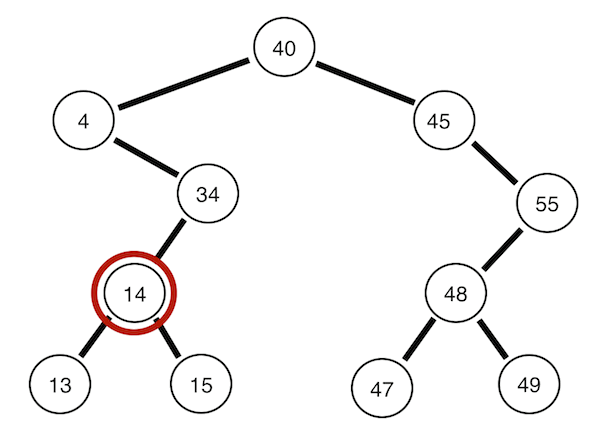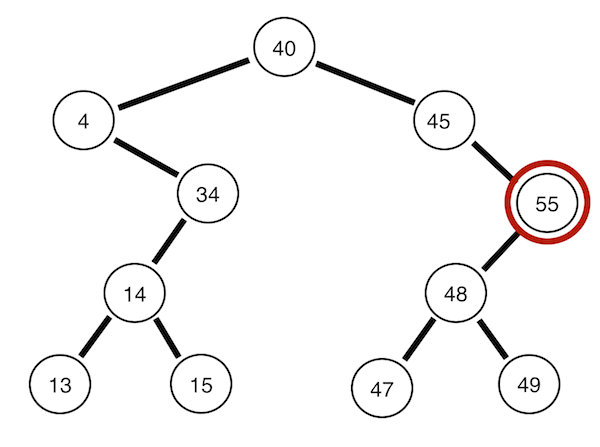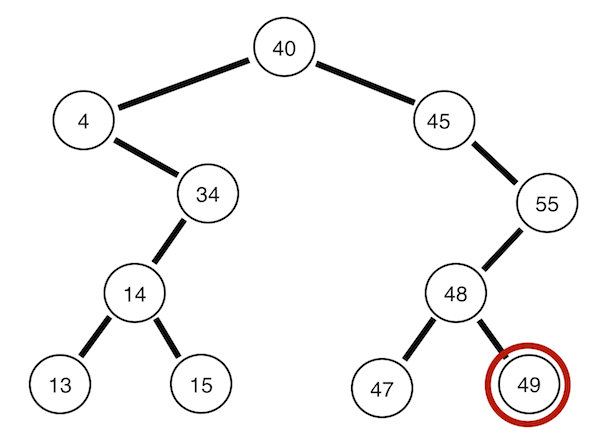
root->left->right의 순으로 트리의 노드들을 돌아보는 방식입니다.
중위 순회

left->root->right의 순으로 순회합니다.
후위 순회
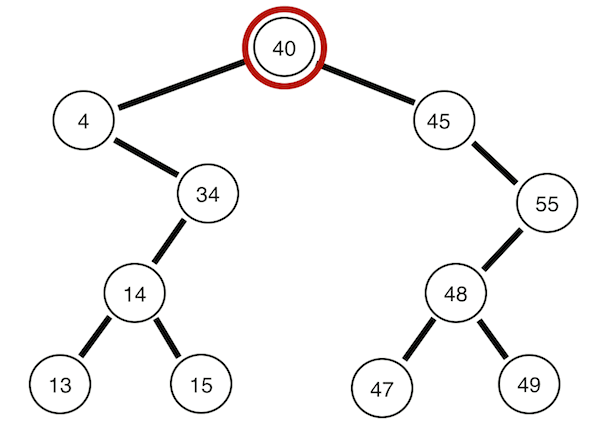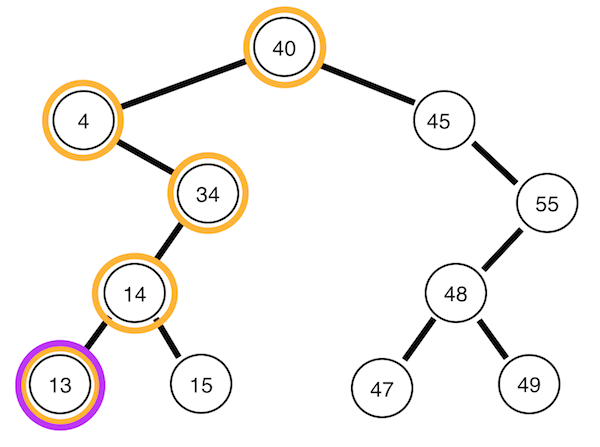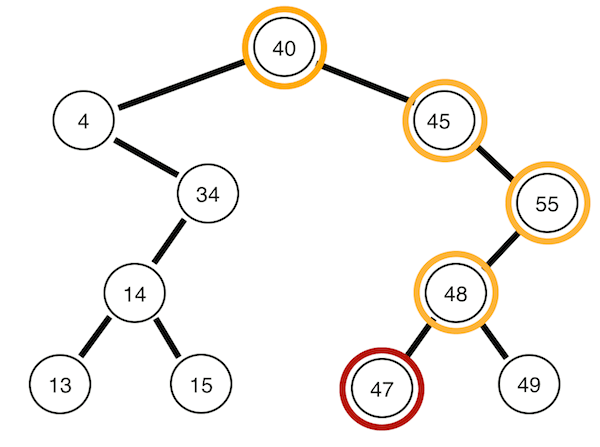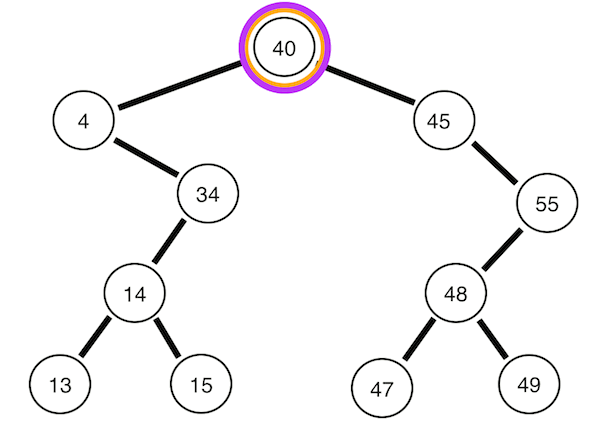
left->right->root의 순으로 순회합니다.
저는 이따가 중위 순회 방식으로 구현해보겠습니다. 해당 코드를 전위, 후위로 바꾸는 것은 복사 붙여 넣기 조립만 잘해주시면 되거든요. 직접 고민해보셨으면 합니다.
BFS
너비 우선 탐색. 레벨 단위로 탐색하는 방식입니다.

손이 부들부들 떨려서 유난히 구려 보이지만 같은 색으로 칠해진 아이들이 동일 레벨입니다. 위 예제에서는 1부터 14까지 순서대로 탐색하겠네요.
일반적으로 dfs는 재귀 혹은 stack으로 bfs는 queue로 구현합니다.
Node 클래스
package hello.core.week5;
public class Node {
private int value;
private Node left;
private Node right;
public Node(int value){
this.value = value;
this.left = null;
this.right = null;
}
public Node(int value,Node left,Node right){
this.value = value;
this.left = left;
this.right = right;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
BinaryTree 클래스
package hello.core.week5;
import java.util.ArrayDeque;
import java.util.Queue;
public class BinaryTree {
public void bfs(Node node){
if(node == null){
return;
}
Queue<Node> queue = new ArrayDeque<>();
queue.offer(node);
while(!queue.isEmpty()){
Node n = queue.poll();
if(n!=null){
System.out.println(n.getValue());
if(n.getLeft()!=null){
queue.offer(n.getLeft());
}
if(n.getRight()!=null){
queue.offer(n.getRight());
}
}
}
}
public void dfs(Node node){
if(node == null){
return;
}
dfs(node.getLeft());
System.out.println(node.getValue());
dfs(node.getRight());
}
}
테스트 코드
package hello.core.week5;
import org.junit.jupiter.api.BeforeAll;
import org.junit.jupiter.api.DisplayName;
import org.junit.jupiter.api.Test;
import static org.junit.jupiter.api.Assertions.*;
class BinaryTreeTest {
static BinaryTree binaryTree;
static Node root;
@BeforeAll
static void create(){
binaryTree = new BinaryTree();
Node n1 = new Node(3,new Node(6),new Node(7));
Node n2 = new Node(2,new Node(4),new Node(5));
root = new Node(1,n2,n1);
/*
1
2 3
4 5 6 7
*/
}
@Test
void dfs(){
binaryTree.dfs(root);
}
@Test
void bfs(){
binaryTree.bfs(root);
}
}
제가 작성한 코드에서 직접 여러 가지 들을 수정해보실 수 있습니다. 일단 테스트 코드에서 트리를 구성하는 방식을 setter를 이용해서 left node와 right node를 직접 붙여줄 수 있습니다. 또한 Binary 클래스에서 중복되는 코드를 따로 메서드로 분리해도 되구요. 아까 언급한 내용처럼 dfs를 중위순회가 아니라 전위나 후위 방식으로 수정해보셔도 됩니다.
간단한 실습 문제 추천드리고 가겠습니다.
1991번: 트리 순회
첫째 줄에는 이진 트리의 노드의 개수 N(1≤N≤26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 영문자
www.acmicpc.net
트리 순회 방식들을 전부 사용해보는 문제로 어려운 응용을 요구하지 않으니 풀어보세요.
'알고리즘 > 이론' 카테고리의 다른 글
| 세그먼트 트리(Segment Tree) (0) | 2021.05.11 |
|---|---|
| 크루스칼 알고리즘 (0) | 2019.05.26 |
| 그래프 표현 방식과 탐색 방법 (0) | 2019.05.19 |
| Dynamic Programming (0) | 2019.05.04 |
| Hash 함수 (2) | 2019.04.30 |
